对该贴进行一些补充和证明。

贪心细节错了很容易意识到，但很多人应该和我一样不知道如何修正。这里写一写供后人食用吧。

考虑下图情况：

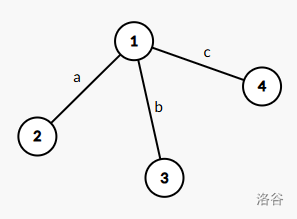
假设 $3$ 节点和 $4$ 节点处各有 $1$ 支军队。叶子节点 $2$ 还未被覆盖。设 $3$ 还剩下的可用时间为 $t$。此时有两种选择：

1. $3$ 的军队去 $2$，$4$ 的军队去 $3$，时间 $\max(a + b, b + c)$。

2. $3$ 呆在原地不动，$4$ 的军队去 $2$，时间 $a + c$。

我们的贪心出错就是因为选择了方案二，但有时候方案一比方案二更优。这种情况发生当且仅当 $\max(a + b, b + c) < a + c$。

即：$b + \max(a, c) < a + c$。

分类讨论如下：

• 若 $a \le c$，则 $b + c < a + c$，得到 $b < a$，即 $b < a \le c$；

• 若 $a > c$，则 $b + a < a + c$，得到 $b < c$，即 $b < c < a$。

发现 $b < a$ 总是成立。

同时有一个限制，$3$ 处军队想要到达 $2$，必须满足 $a + b \le t$。由于 $b < a$，$t > 2b$。

所以，当 一支到达了根节点儿子的军队 所剩下的时间 大于 其到根节点距离的两倍，我们可以选择方案一，且此时方案一比方案二更优。

这也就解释了为何如下 Hack 的答案为 $100$ 而非 $198$。

4
1 2 99
1 3 1
1 4 99
3
3 4 4

具体实现的话加一句 if 判断一下即可。